User:Joger/Color Management

This document contains personal draft notes on color management topics, and can not be considered a reference on the topic.

The CIE 1931 XYZ color space

CIE 1931 chromaticity diagram

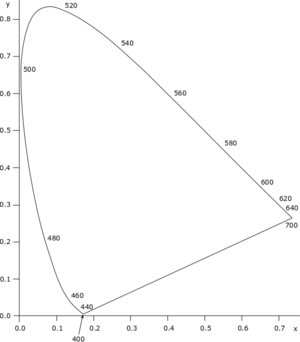
The CIE XYZ 1931 color space lays the foundation for understanding color management concepts such as color spaces, gamut, white point, and transfer functions. Specifically, the CIE color space defines a generic color coordinate system that is used do define other color spaces. This coordinate system consists of three axes, with coordinates x, y, and z. Usually, the z axis is projected onto the x-y plane and looks like the characteristic shark fin. At around its locus we find the colors that corresponds to a monochromatic light source when it is swept from 400 nm to 700 nm.

The point of the CIE 1931 XYZ color space is that it gives every visible color a well-defined (x, y) coordinate. This is important when we derive other color spaces, such as the sRGB color space, because concepts such as primary colors, gamut, and white point are defined based upon the corresponding (x, y) coordinate in the CIE coordinate system. Having a common reference becomes particularly important when we need to convert between different color spaces.

Derivation of the CIE XYZ coordinate system

CIE 1931 matching functions

The idea behind the CIE 1931 XYZ color space is that to be able to reproduce colors, a camera needs 3 different sensors, each responding to different wavelengths of light. Since light exists across a spectrum of frequencies, such sensors needs to respond to a wide range of wavelengths, although its sensitivity is highest at a specific frequency, and falls off for higher and lower frequencies. The CIE 1931 matching functions X(λ), Y(λ) and Z(λ) defines the response of a 3 sensor camera that is able to capture all visible colors, and these matching functions defines the CIE color space. We find the response of a single sensor as an integral over the spectrum of the light source and its corresponding matching function. For example, if a source emits light in a spectrum between 560 and 660 nm, a sensor with the characteristics of the X(λ) or Y(λ) matching functions will get a response, whereas the sensor following the Z(λ) matching function will have almost no response.

Given an input spectrum of light (colors), we calculate the CIE tristimulus values X, Y, and Z by accumulating its emission power at each discrete frequency, weighted by the corresponding CIE 1931 matching function. If an analog sensor was following perfectly one of the matching functions, the calculated value would roughly correspond to the output voltage of the sensor.

In color management, it is beneficial to remove the absolute power of the output values by normalizing them against the total power from all the sensors:

x = X / (X + Y + Z) y = Y / (X + Y + Z) z = Z / (X + Y + Z)

The x, y, and z values are known as CIE chromaticity, and the x and y coordinates corresponds to the axes of the CIE 1931 chromaticity diagram. In practice z is redundant because x + y + z = 1. Also note that the x, y, and z chromaticity coordinates are abstract values, and have no direct physical interpretation.

Luminance

Luminance, denoted Y, unit cd·m^-2 (nits) is a linear light quantity that is loosely coupled with what we think of as brightness. The luminance of a light source is calculated by accumulating its power over its spectrum, weighted by the Y(λ) CIE color matching function. It turns out that this function agrees well with how humans perceive brightness. Mid-range green values will contribute more to the response than red and blue, but all visible colors contribute. For example, if we have three light sources, red, green, and blue, and they each emit the same power, the green light source will appear the brightest, while the blue light source will appear the darkest. This means that formulas that calculates luminance from R, G, and B values, will put more weight on green colors than the other primaries, as shown in the Rec. ITU-R BT.709 which standardizes some classes of displays:

⁷⁰⁹Y = 0.2126 R + 0.7152 G + 0.0722 B

Here, luminance gets 21% of its power from red, 72% of its power from green, and 7% of its power from blue. Note that luminance is typically not used in video processing, because we rarely intend to reproduce the absolute luminance of the actual scene.

Relative luminance

The unit of X, Y, and Z is often arbitrarily chosen so that Y = 1 or Y = 100 is the brightest white that a color display supports. In this case, Y is a relative luminance . Relative luminance is a unitless quantity, and is proportional to the scene luminance up to the maximum luminance of the screen/device.

The sRGB color space as defined within a CIE XYZ color space

Color spaces

Now that we have a reference color space, we can start defining other color spaces which are subsets of the CIE XYZ color space. The Rec. 709 defines a standard for HDTV screens, including their color space.

This standard defines the white point to be at x = 0.31271 and y = 0.32902, which is known as D₆₅. This means that a color at this coordinate is considered the 'reference' white on HDTV screens, and is engineered such that equal amounts of R, G, and B primaries will appear white for a reference observer in a reference environment.

In addition, the standard defines the color primaries, or primaries for short. The primary blue color is at x = 0.15 and y = 0.06, red is at x = 0.64 and y = 0.33, while green is at x = 0.30 and y = 0.60 as illustrated in the CIE chromaticity diagram. The primaries denotes the maximum red, green, or blue that the screen can display. The triangle spanned by the three primaries are called the gamut, and the screen can only display colors within this triangle. Any color within the gamut is created by adding different amounts of the primary colors.

Gamma correction and transfer functions

Gamma compression and expansion at gamma 2.2

Gamma correction or just 'gamma' is a nonlinear operation used to encode and decode luminance or tristimulus values in video or still image systems. Its origin comes from the way CRT screens worked, where the luminance produced at the face of the display is a non linear function of each (R', G', and B') voltage input. By coincidence, this is beneficial because the human vision is more sensitive to differences in dark colors than bright colors. In digital imaging we can utilize gamma compression to make better use of our bits by converting input values into a perceptually uniform space. In a perceptually uniform space, the perceived difference in lightness between RGB values (10, 10, 10) and (20, 20, 20) should be equal to the difference of RGB values (210, 210, 210) and (220, 220, 220) after expansion through the decoding gamma.

Gamma correction can be expressed as:

V_out = AV_in^gamma

If the inputs and outputs are in the range [0...1], A = 1. A gamma < 1 is sometimes called an encoding gamma, and encoding a signal with this gamma is called gamma compression (V_comp in the picture). Gamma compression was originally introduced on the imaging side to counteract the expansion made on the display side. A gamma > 1 is referred to as decoding gamma, and decoding a signal with a decoding gamma is called gamma expansion (V_exp in the picture).

'Note: The input to gamma compression is tristimulus values (linear light) as captured by an imaging device. Such values are denoted R, G, and B. The output of the gamma compression is a gamma-corrected video signal is denoted with a prime symbol, and is written R', G' and B . If a letter related to color management has the prime symbol, it means that the value is non-linear. For example, if we see the symbol Y', this means that this is the luma derived from a gamma compressed signal, not the luminance of the input tristimulus values. In computer graphics, this is an important distinction. For example, (incorrectly) averaging two compressed pixel values does not yield the same result as (correctly) averaging two uncompressed tristimulus values.

Luma, denoted Y' , is calculated as a weighted sum of gamma corrected R', G', and B' components. Luma is therefore not a linear quantity.

Transfer functions map numerical coordinates to and from a color space. The transfer functions can be linear, or non-linear. Typical examples of non-linear transfer functions are Gamma 2.2 and the non-linear transfer function defined by sRGB .